|
Two Distance To Brake To Stop Formulae means the Bicycle Brake Stop Calculator calculates in each worksheet of the Excel spreadsheet 'StoppingDistance.xls' both the Distance To Brake To Stop and Time To Brake To Stop for different example velocities, V, and gradients, G. |
||
| Stopping Sight Distance or Distance To Brake To Stop = Brake Reaction Distance + Brake Response Distance | ||
| Brake Reaction Distance = Velocity in metres p/s x Brake Reaction Time of 2.5 secs | ||
| Brake Response Distance = Velocity in metres p/s x Brake Response Time x Ave Braking Speed of initial V divided by 2 | ||
|
||
|
|
|
|
|
Below is an explanation of the above listed
1st
Distance To Brake
To Stop Formula
for 5 different Velocities (speeds) between 30km p/h to 80km p/h and from a flat
roadway to a 20% descent gradient which are calculated in 5 separate worksheets
in Bicycle Brake Stop Calculator
Excel spreadsheet
'StoppingDistance.xls'.
Each of those 5 worksheets also calculate the
Distance to Brake to Stop
using the above
2nd
Distance To Brake To Stop Formula
of |
|
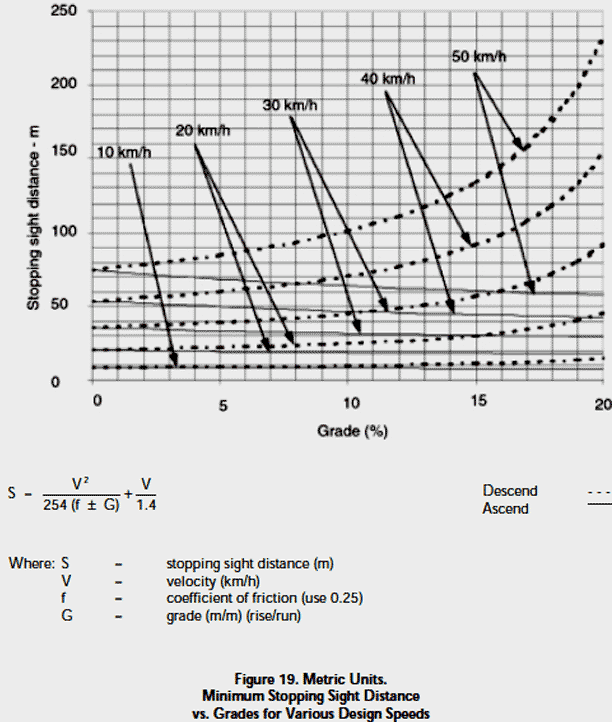
1. Rationale to calculate the Distance to Brake to Stop for a bicycle travelling at 20km/p/h on an ascent sloping 5% - see worksheet 'stop_distance_calc 20km +5%' in 'StoppingDistance .xls' which calculates using the formula on the LHS (of the worksheet) and the formula in the above LHS Figure 19 to calculate both the Distance to Brake to Stop and the Time to Brake to Stop. 20 km/p/h is
20,000 metres per 3,600
seconds, or 5.556 metres per second. |
|
2. Rationale to calculate the Distance to Brake to Stop for a bicycle travelling at 20km/p/h on a level road - see worksheet 'stop_distance_calc 20km 0%' in 'StoppingDistance .xls' which calculates using the formula on the LHS (of the worksheet) and the formula in the above LHS Figure 19 to calculate both the Distance to Brake to Stop and the Time to Brake to Stop. 20 km/p/h is
20,000 metres per 3,600
seconds, or 5.556 metres per second. |
|
3. Rationale to calculate the Distance to Brake to Stop for a bicycle travelling at 40km/p/h on a level road - see worksheet 'stop_distance_calc 40km 0%' in ''StoppingDistance .xls' which calculates using the formula on the LHS (of the worksheet) and the formula in the above LHS Figure 19 to calculate both the Distance to Brake to Stop and the Time to Brake to Stop. 40 km/p/h is 40,000 metres per 3,600
seconds, or 11.11 metres per second. |
|
4. Rationale to calculate the Distance to Brake to Stop for a bicycle travelling at 30km/p/h on a descent sloping 10% - see worksheet 'stop_distance_calc 30km -10%' in ''StoppingDistance .xls' which calculates using the formula on the LHS (of the worksheet) and the formula in the above Figure 19 to calculate both the Distance to Brake to Stop and the Time to Brake to Stop. 30 km/p/h is 30,000 metres per 3,600
seconds, or 8.33 metres per second. |
|
5. Rationale to calculate the Distance to Brake to Stop for a bicycle travelling at 50km/p/h on a descent sloping 20% - see worksheet 'stop_distance_calc 50km -20%' in ''StoppingDistance .xls' which calculates using the formula on the LHS (of the worksheet) and the formula in the above LHS Figure 19 to calculate both the Distance to Brake to Stop and the Time to Brake to Stop. 50 km/p/h is
50,000 metres per 3,600
seconds, or 13.89 metres per second. |
|
6. Rationale to calculate the Distance to Brake to Stop for a bicycle travelling at 70km/p/h on a descent sloping 12% - see worksheet 'stop_distance_calc 70km -12%' in ''StoppingDistance .xls' which calculates using the formula on the LHS (of the worksheet) and the formula in the above LHS Figure 19 both the Distance to Brake to Stop and the Time to Brake to Stop. 70 km/h is
70,000 metres per 3,600
seconds, or 19.44 metres per second. |
|
7. Rationale to calculate the Distance to Brake to Stop for a bicycle travelling at 80km/p/h on a descent sloping 15% - see worksheet 'stop_distance_calc 80km -15%' in ''StoppingDistance .xls' which calculates using the formula on the LHS (of the worksheet) and the formula in the above LHS Figure 19 to calculate both the Distance to Brake to Stop and the Time to Brake to Stop. 80 km/h is 80,000 metres per 3,600
seconds, or 22.22 metres per second. |
On a road sloping downhill at -
* 20%, with a 0.25 Coefficient Of Friction, most of the braking force will be absorbed by counteracting gravity, thereby leaving relatively little of the braking force available to slow the bike, so it will take a very long time to stop.
* 25%, with a 0.25
Coefficient Of Friction, the entire braking force will be needed to counteract the gravitational acceleration, the bike will continue at a constant speed and the braking distance will be infinite.However, the above calcs make no allowance that a heavier cyclist will take longer to brake to a halt than a lighter cyclist.
In dry conditions a heavier cyclist will take longer to stop than a lighter cyclist. This is because the Coefficient Of Friction will be higher, and thus allow higher braking forces. These higher braking forces will cause the brakes to heat up and fade, or cause the brake pads or the rubber on the tyre to start to shred. In wet conditions the braking forces will be lower and the brakes will be less likely to overheat.Sight Distance - pg 40 of 'Guide for development of bicycle facilities" notes:
The distance required to bring a bicycle to a full controlled stop is a function of the -
i) bicyclist’s perception time;
ii) bicyclist's brake reaction time,
iii) initial speed of the bicycle, known as V
iv) coefficient of friction between the tires and the pavement - known as f, and
v) braking ability of the bicycle and rider, known as Ab.
Four other variables which affect the Distance to Brake to Stop and the Time to Brake to Stop are the -
vi) gradient of road ahead during Distance to Brake to Stop known as G
vii) weight of the bicycle and rider, known as M; and
viii) direction of road ahead during Distance to Brake to Stop known as Dir;
viii) wind direction and strength, known as W.
The above are known as the Eight Bicycle Variables To Stop.
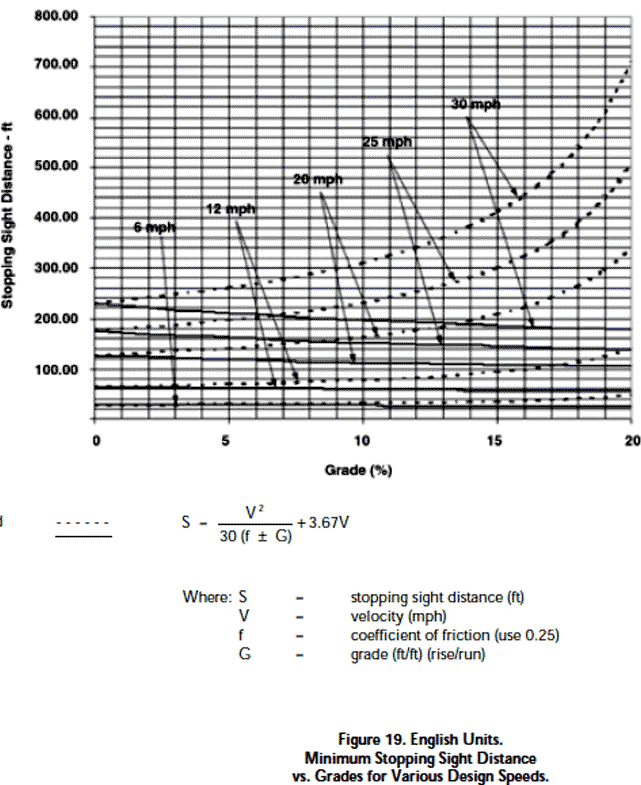
The two below Figure 19 indicates the minimum stopping sight distance (separately in km and then miles), referred to in this analysis as the Distance to Brake to Stop, for various design speeds and grades based on a bicyclist's brake reaction time of 2.5 seconds and a Coefficient Of Friction of 0.25 to account for the poor braking equipment of many bicycles and limited skills of.
As noted in Bicycle Brake Stop Calculator -
(A) presently the Bicycle Brake Stop Calculator -
(a) assumes a constant Mass of the cyclist is 150lbs (68.1kgs) and assumes a Coefficient Of Friction f of 35%;
(b) factors in only the variables of speed V and gradient G.
(c) does not factor in the variables 4, 5, 6 and 7 of the Eight Bicycle Variables To Stop. These are:
direction of road ahead (between 0 degrees and 90 degrees) is Dir
bicycle/cyclist weight = Mass is M
wind speed impact is W
braking ability of the bicycle and rider is Ab
(B) It should be possible to incorporate the above 'missing' variables to test the Two Distance To Brake To Stop Formulae.
by Wayne Pein wpein@nc.rr.com (Revised July 2007) notes that according to AASHTO’s “Green Book,”A Policy on Geometric Design of Highways and Streets, in roadway design, braking and sight distance calculations for all vehicles, including bicycles, are figured using a deceleration rate of 3.4 m/s2 (11.2 ft/s2), which is 0.35 g.Four-wheeled motor vehicles have much better emergency braking capabilities than bicycles, approximately 0.6 - 0.7 g (some cars can achieve more than 0.9 g), affording motorists a great margin for error beyond AASHTO’s roadway design specification. In contrast, a typical bicyclist can be expected to decelerate at 0.35 g on clean, dry, level pavement which, coincidentally, is AASHTO’s figure for roadway design purposes as previously noted. A conventional bicycle's theoretical maximum deceleration is limited to about 0.6 g on level pavement by weight transfer, which can cause pitch-over. However, only a highly skilled bicyclist using optimal technique may be able to achieve this 0.6 g; most will be far lower at about 0.35 g.
For non-level roads the grade is added (+ or -) to this deceleration rate in gees. This means that on a 5% descent, for example, braking effort equivalent to 0.05 g is used to counteract the effect of gravity, leaving typical bicyclists only 0.35 - 0.05 = 0.30 g for deceleration.
Further, unlike motor vehicle braking which is not markedly affected in wet conditions, the braking capability of some bicycles is greatly reduced due to the diminished friction between the brake shoes and a wet rim. According to John Forester [personal communication, 12/22/04] “Bicycle braking under wet conditions needs to be considered in two phases. The first phase is wiping the rims clean, the second phase is actual braking. For aluminium rims, one can consider three rotations of the wheel to wipe the rim reasonably dry. That is about 21 feet for typical wheel sizes. Subsequent braking, given good brakes to start with, is then typical of dry, unless the road surface is so slippery that it will not produce a 0.67 Coefficient Of Friction. The situation with chrome-plated steel rims is worse; they don't wipe dry.”
At 20 mph (29 ft/s), 21 feet of nearly nonexistent braking adds about 0.7 seconds to braking time. Thus, instead of taking 2.6 seconds to come to a complete stop, it would take 3.3 seconds on level ground when wet, amounting to an average deceleration of 0.28 g. Heavy rain or road splash at high speed could result in continuously wet rims, further drastically reducing braking capacity.
For sight-triangle and other operational calculations, bicycle deceleration rate in wet conditions should be considered to be slightly more than half that under dry conditions; 0.20 g.
Moreover, BL stripes are very slippery when wet, adding an unnecessary longitudinal hazard.
These concerns amplify the argument that BLs are counter-indicated, especially on high speed descents.
NOTES ON RESISTANCE AND POWER IN CYCLING
The standard model for calculating the resistance to motion of bicycles, using pounds, feet, and seconds, is:
Resistance (lbs) = Slope Resistance + Rolling Resistance + Air Resistance
Slope Resistance =Mass * Slope
Rolling Resistance =Bearing Friction + Tire Losses (both empirically determined)
Air Resistance =Density of air/2 * Cross Sectional Area * Drag Factor * Speed * Speed
The accepted standard density of air at sea level is 0.002378 slugs/cu.ft. (Which equals 0.07657 lbs/cu.ft)
The FHWA research done in Davis (FHWA-RD-75-112) gives the following resistances when using a system that uses pounds and hours and mixes feet with miles:
Resistance, lbs (FHWA) =Weight*Slope + Weight*(0.005 + 0.15/TirePressure) +
0.00256*(AirSpeed*AirSpeed*DragArea* DragFactor)
The 0.00256 factor converts the 0.002378 by combining the division by 2 and the conversion from feet per second to miles
per hour. Also, their values for bearing and tire friction are high relative to what is available today. Good wired-on tires
have improved greatly since then. The CycSpeed program reflects this change by using bearing friction of 0.002 and tire
losses as 0.10/TirePressure.
Whitt and Wilson give the following for typical drag areas and factors:
Cyclist on roadster bicycle: 5.3 Square Feet and 1.2 Drag Factor
Cyclist on sporting bicycle: 4.3 Square Feet and 1.0 Drag Factor
Cyclist on racing bicycle: 3.55 Square Feet and 0.9 Drag Factor
The resistance to acceleration (inertia) is greater than the mass by an amount very nearly equal to the mass of the tires
and rims. CycSpeed adds in the masses of the tires and rims. Whitt & Wilson call this the WheelResistanceFactor and
typically give it a value of 0.01 for all bicycles.
Whitt & Wilson give the following for resistance using metric (MKS) system:
Res (newtons) = Mg(Rolling Resistance + Slope Resistance + Wheel Resistance Factor) +
0.5*(Drag Factor*Drag Area*Air Density*Airspeed*Airspeed)
=Mg*(Cr + slope + a/g*1.01) + 0.5*Cd*A*R*(Vc + Vw)*(Vc + Vw)
=Mg*(Cr + slope + a/g*1.01) + 0.5*1.0*0.4*1.226*V*V
=K1 + K2V*V +10.32M(slope +a/g*1.01)
Where K1 and K2 are per the following:
K1 K2
Roadster bicycle 7.845 0.3872
Sports bicycle 3.509 0.2581
Racing bicycle 2.508 0.1916